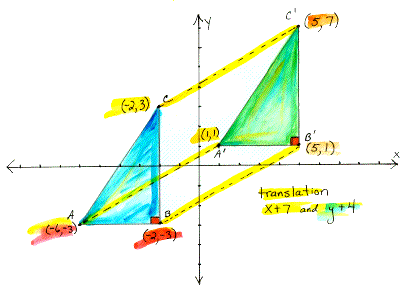Aim: How do we graph rotations? 

• Rotation is when an image is rotated from one point with the same distance. So here are some rules when it comes to rotating. 

1. 90 degrees:   (x,y)     →  (-y,x)
2. 180 degrees: (x,y)    →  (-y,-x)
3. 270 degrees: (x,y)    →   (y,-x)

• These rules are for counter-clockwise, except for 180 degrees. Now if a problem asks for clockwise, you should use the rule that is opposite. For example:

1. If it says "90 degrees clockwise", you could use the rule for 270 degrees counter-clockwise. 
2. If it says "270 degrees clockwise", you could use the rule for 90 degrees counter-clockwise. 

This globe/earth is going
360 degrees counter-clockwise.

• This is because if you look at a clock and try what a question is asking, it'll make sense. Just because if your going 90 degrees clockwise, it'll be the same as going 270 counter-clockwise. And if your going 180 degrees, it'll be the same either counter-clockwise or clockwise. 

Now try it yourself ! 

     ↓

Aim: How do we use the other definitions of transformations?

There are 4 main types of transformations, but there are many more. The main four are:

• Rotation:  The distance from the center to any point on the shape stays the same.

This ballerina is rotating
360 degrees consistantly.
She is rotating from her heel
on her left foot.

• Translation:  When an image moves by changing it's coordinates by equal distance, same direction, and that the figure stays the same size.

A students drawing of  their
ΔABC being translated by T(7,4).

• Reflection: when an image is reflected over a line to create a mirror image. 

The woman in this picture is
being reflected by the
lake in front of her.

• Dilation: when an image is enlarged or shrunk from its original being. 

The image that Homer is
holding, is the image that
the screen keeps
dilating into.

                           

This person's pupil is
dilated due to being horrified.

                                   
There are many more transformations out there ! But try this little problem:

Aim: What is Isometry?

• The definition of Isometry:

                                - Basically the distance from an original figure (& it's points) and their transformed figure (& their points). 

An example of how ΔABC's points are equally distanced
from  ΔA'B'C' points. This is shown by translation. 

• From the types of Transformations only Reflection, Rotation, and Translation are isometries. Dilation on the other hand, is not a isometry.

                

This earth figure is isometry
b/c each half of the earth
is equal distance from
the other half. 

• The reason why dilation isn't a isometry is because the original image is either shrunk or enlarged. 

Example of  dilation, where
ΔABC is dilated by the
scale factor of 2.

• Now you try it, with this question :

What isometry maps figure 1 to figure 3?

Choices:

A.          reflection 

B.       translation 

C.            rotation 

D.  none of these 

                                       

Aim: How do we graph dilations?

• Dilation is another main function of the transformations. Dilation: 

                      - is the ratio of an image or figure shrinks or enlarges from its original state of being [original size]. This is also known as a Scale Factor.

This is an example of dilation,
b/c the magnifying glass is making
the print look much bigger
through it's lens.

• When it comes to graphing dilations, you have to look at the Scale Factor. 

          

In this image ΔABC is dilated
 bigger to form ΔA'B'C'.
This shows that the scale
factor is bigger than 1. 

*Hint:

                      -If the scale factor is larger than 1, the image 

                        or figure has been enlarged [made bigger].

                       -If the scale factor is greater than 0 and less than 1, 

                   the image or figure has been shrinked. 

• When you're trying to solve any problem that has given you the ratio (scale factor) and original image, you multiply the ratio to the points given. 

An example of dilation in
real life. When  a  person is
excited or scared, their muscles
in their eyeballs stretch.

Aim: How do we graph transformations that are reflections ?

• Reflections is one of the  functions in Transformations. 
• You can go by the definition of Line Reflection:

                                          - A transformation that creates figures which are mirror images of the original.      

                                         
                     

If you look closely at the bubble,
it shows a line of symmetry going horizontally.
That's why the house looks kind of twisted !

                                              


                             

                                    * Trick Rule: -Over the x axis (x,y) -->> (x,-y)   

                                                                           -Over the y axis (x,y) -->> (-x,y)                                                

                

• and the definition of Reflection itself: 

                                          - When a figure is flipped over a line of symmetry. 

    

The red line that goes horizontally
is the line of symmetry to the triangle. 

                 


                    

                       So when you transform a figure by reflection, you use the Line Reflection rule on the point(s). 


Now try it, with this ! *pointing down*