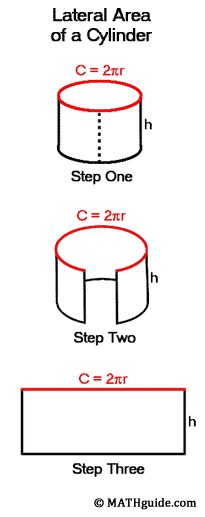
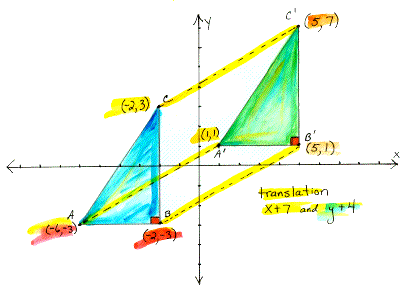- So like last time's review, the surface area is the outside of a solid. So here we'll be working with solids like pyramids & cones. The similarity between these two solids is that they both have triangle(s).
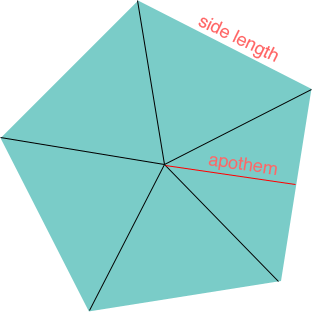
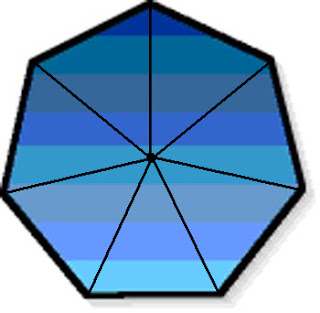
- Pyramids have triangles as the lateral area and only one face. This face can be any shape, from a circle (cone) to a heptagon (7 sides).
- A pyramid in general is a solid that connects a polygon base to a point, called the apex.
- For the surface area & lateral area this is the formula.
- But remember this is only for a square pyramid. For any base use the formula of 1/2pl (perimeter x slant length) + B (area of the base).
- For a cone it's the same, but its for a circular base.
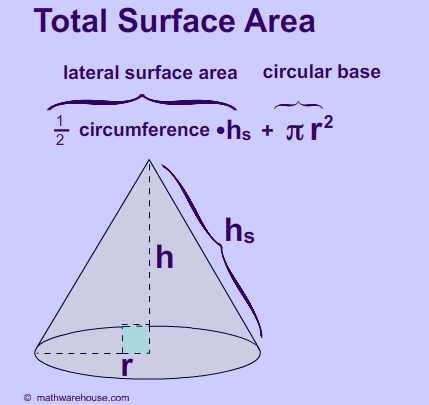
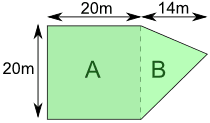
- Well that's about it. So try this problem !
What is the total surface area of this cone, rounded to
the nearest tenth ?

Sources Cited:


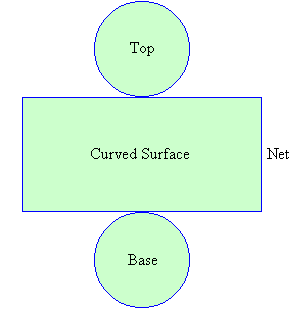









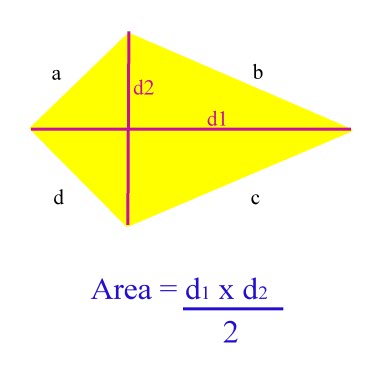
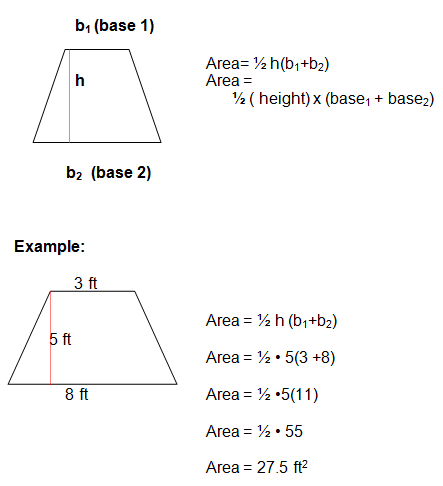
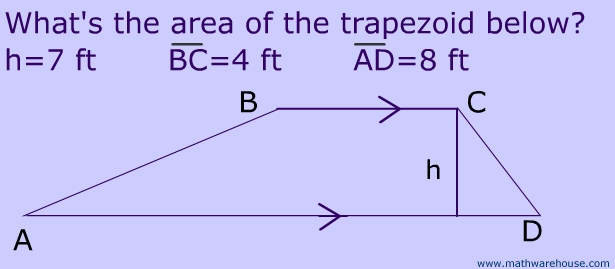


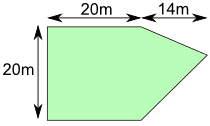












.gif)